上 円の面積 応用 中学 314315

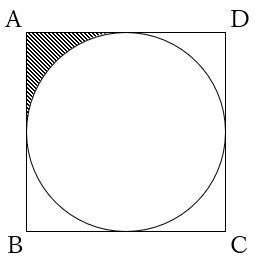
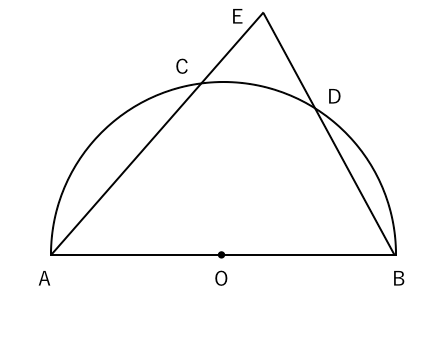
等積変形を応用して典型題を解こう ヒポクラテスの月 も簡単にわかる 中学受験ナビ
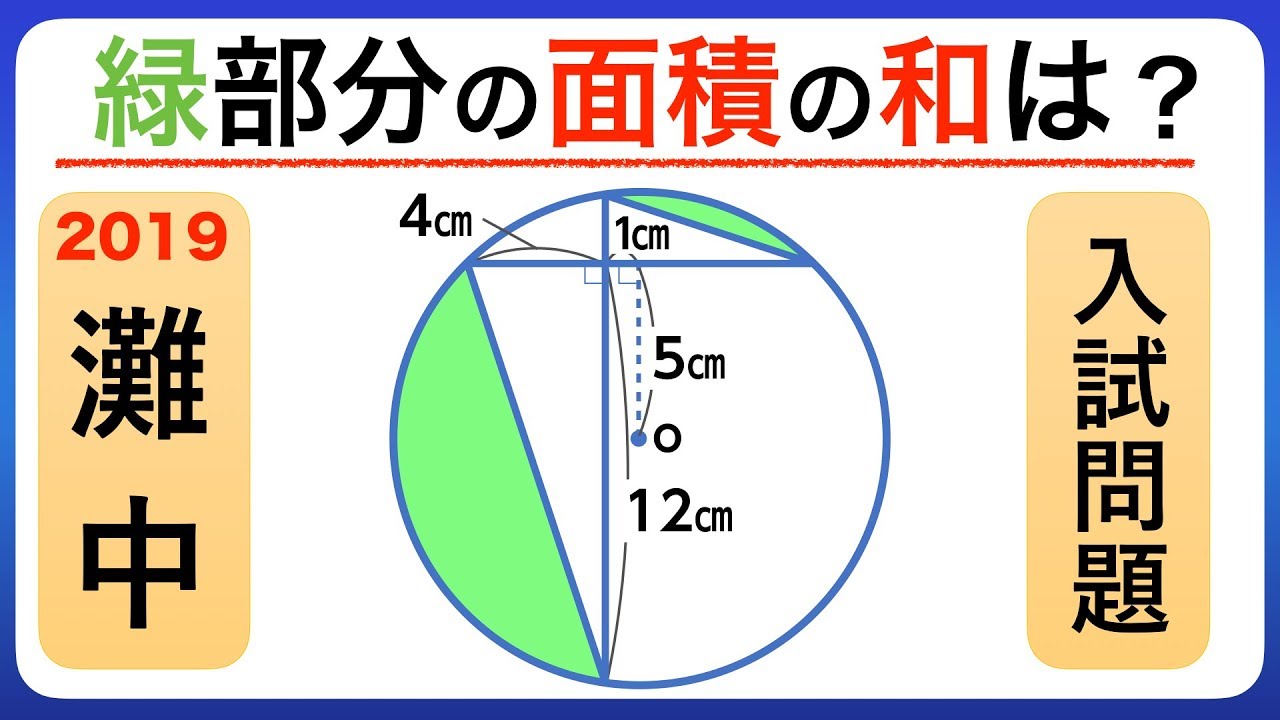
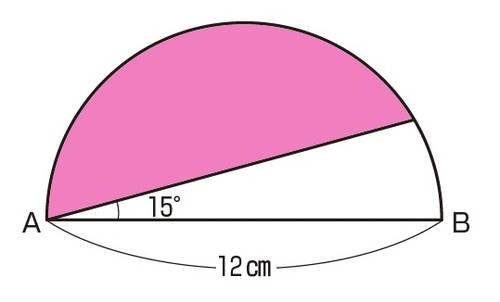
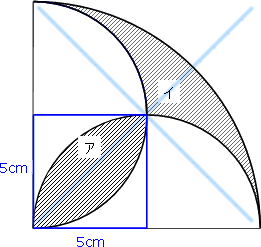
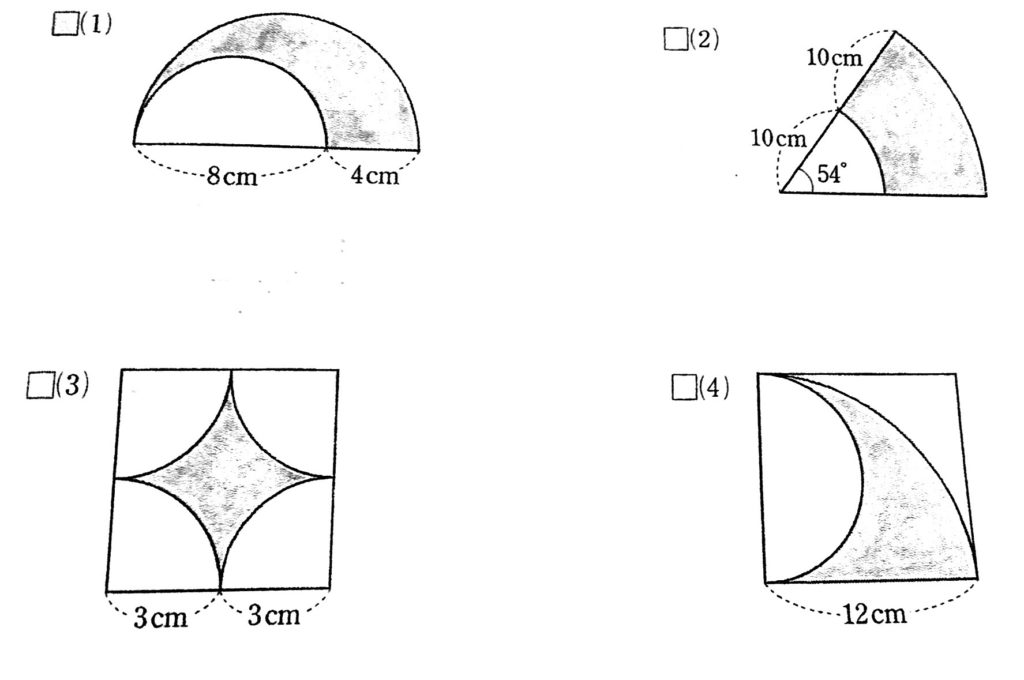
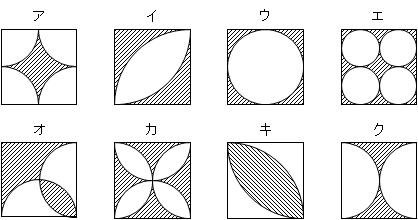
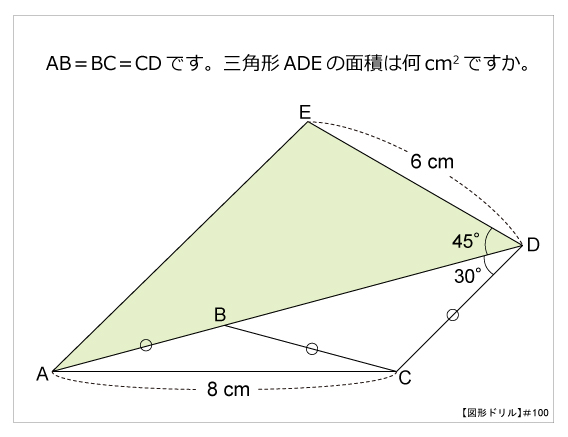
中学受験算数問題(円の面積) 中学受験算数問題(ヒポクラテスの三日月) 中学受験算数(正方形の回転) 木の葉形の面積(1997 灘中 改題) 木の葉形面積(灘中1998 類題) 平面図形の面積(灘 07) 正三角形と正六角形 平面図形の面積 (三田学園A 360 扇形の面積: πr2 ×
円の面積 応用 中学
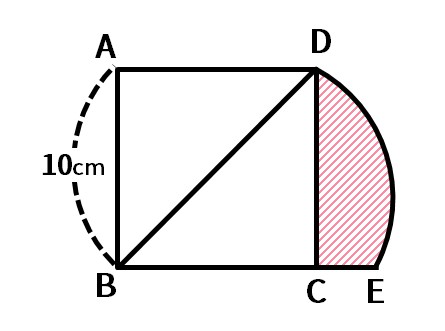
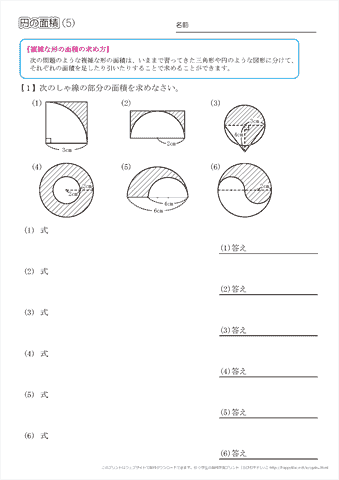
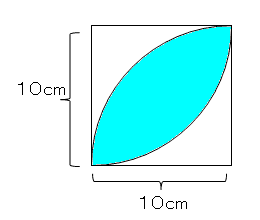
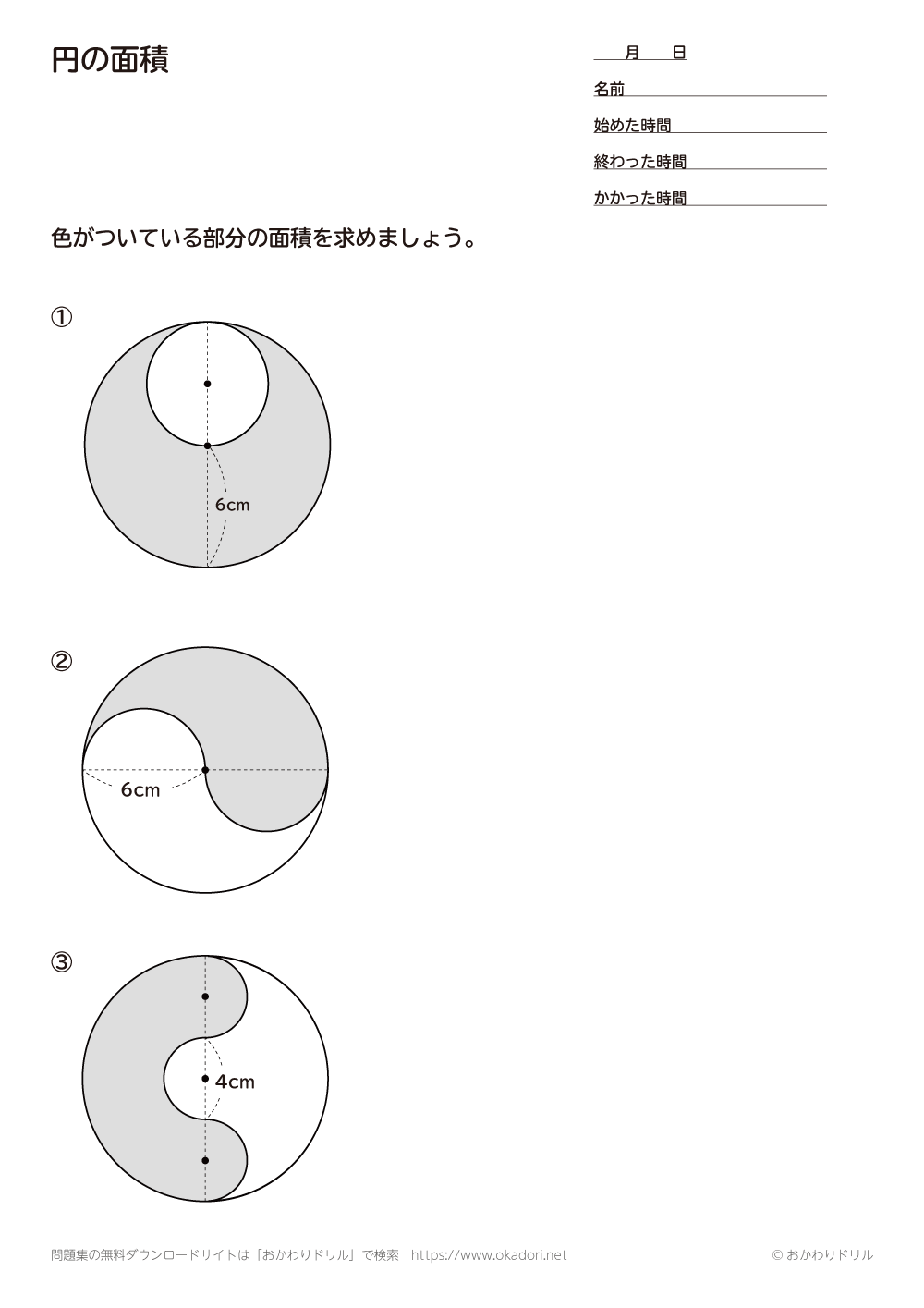
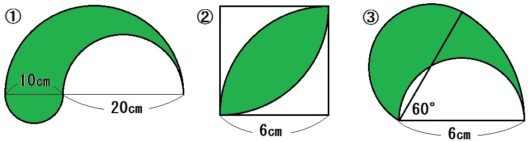
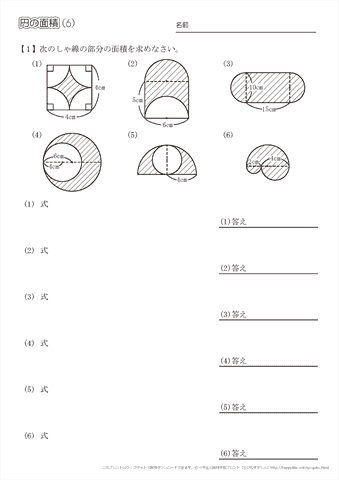
円の面積 応用 中学-半円の周りの長さや、円や図形を組み合わせた問題などが出題されます。 簡単な問題が出来るようになったら、中学入試レベルの応用問題も取り組んでみてください。 ポイント 半円の周り長さは直径の部分も忘れずに求めましょう。 半円の周りの長さ円の面積の求め方を一通り身につけたら、少し応用的な問題にも挑戦してみましょう。 円の面積の応用問題をやってみよう 円の面積の、もっと基本的な問題のノート例はこちらです。 円の面積その1 それでは、

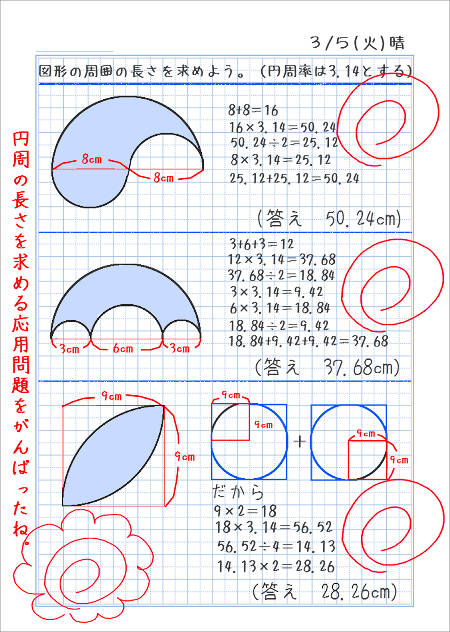
半円を回転させる面積の問題 プリントを使って自分で解こう
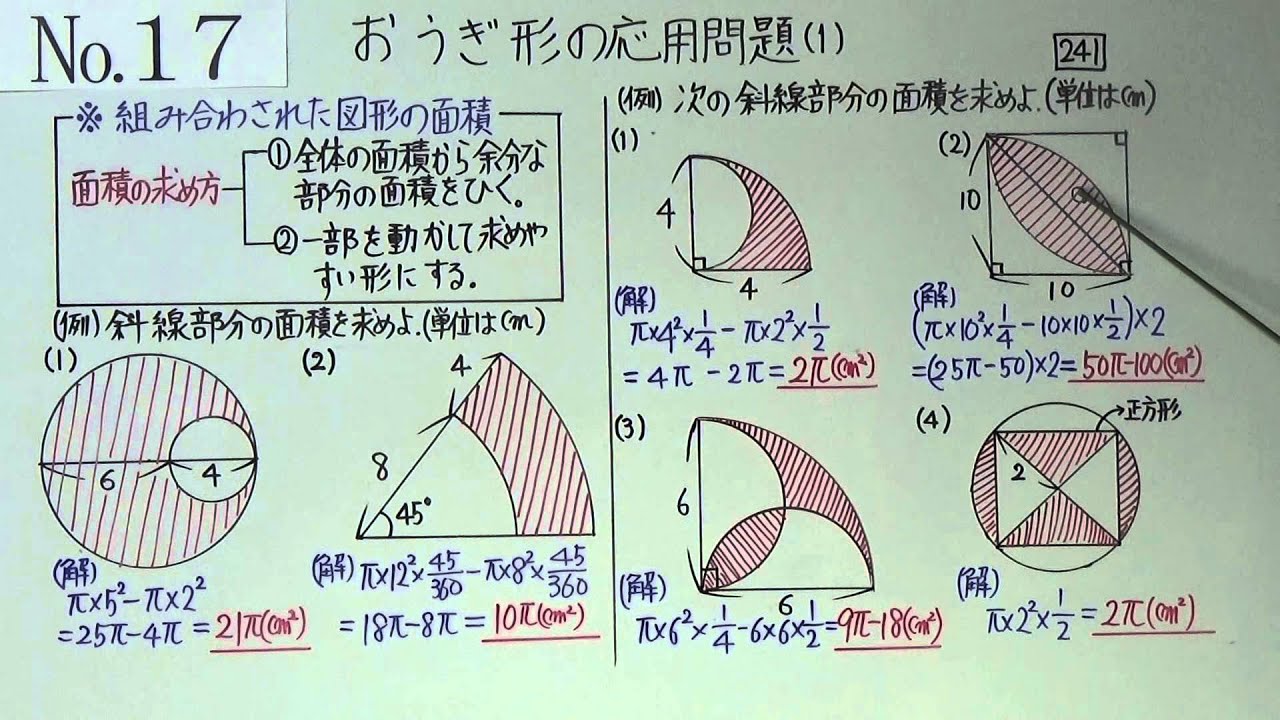
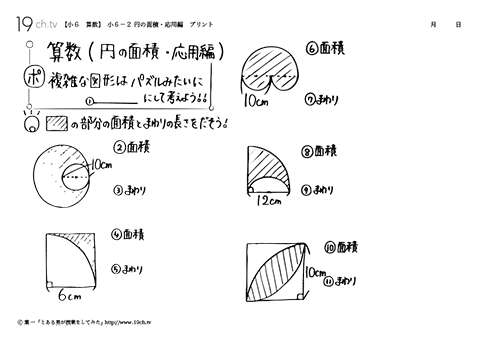
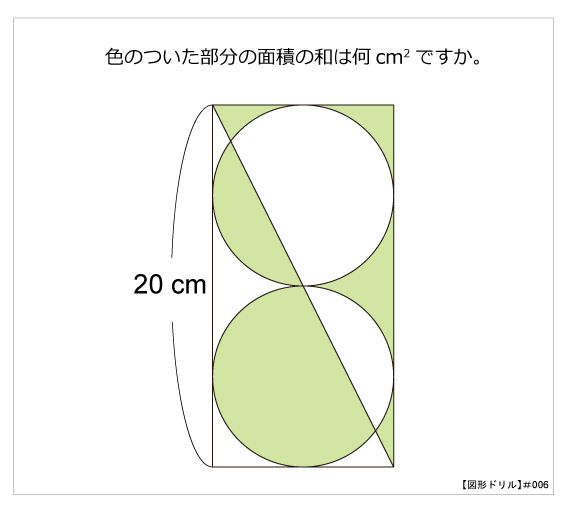
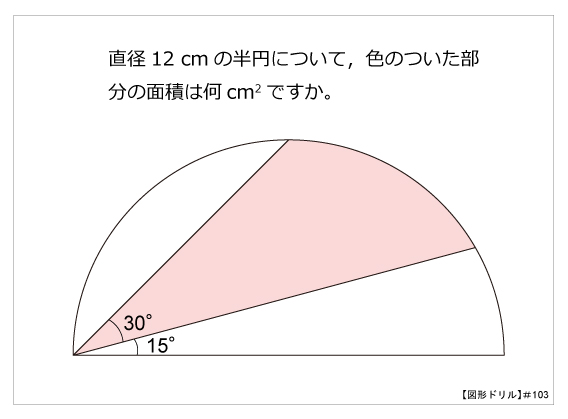
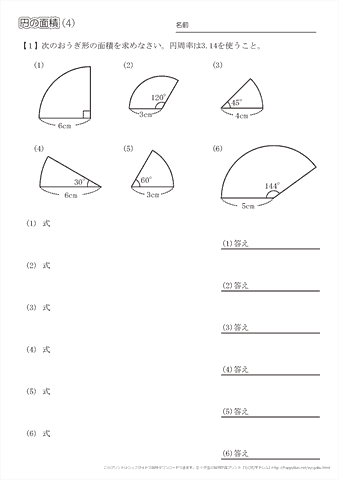
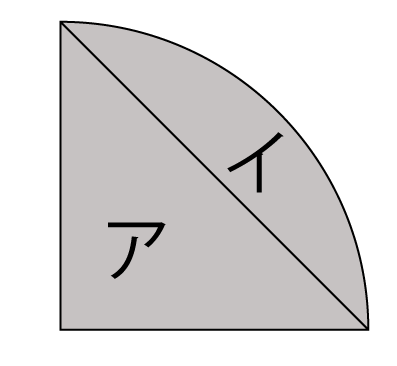
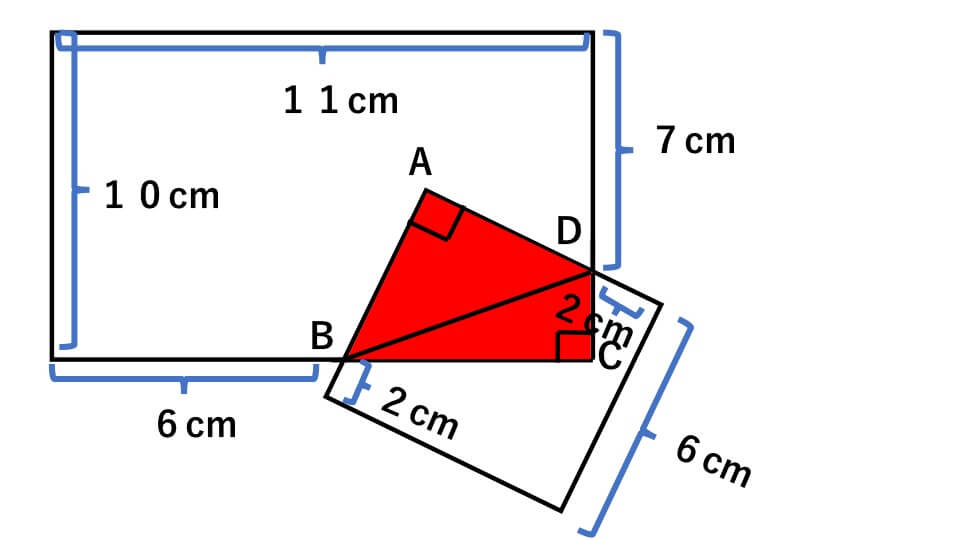
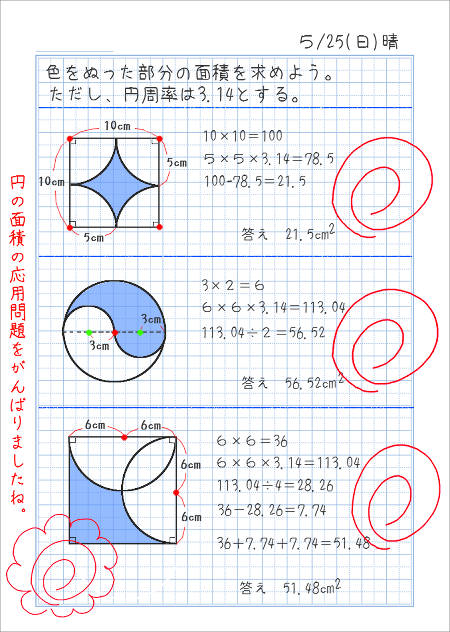
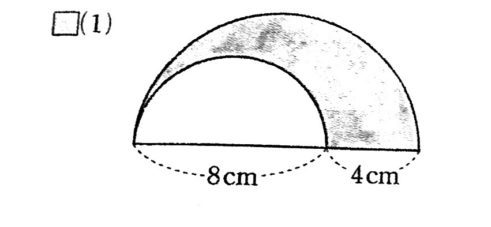
採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引くA 360 π r 2 ×第12問 円の9等分する点 5年生 6年生 三角形 円 角度 ★★★☆☆☆(中学入試標準レベル) 図形ドリル 第13問 四角形の面積 5 blog算数星⼈の中学受験お役立ち情報
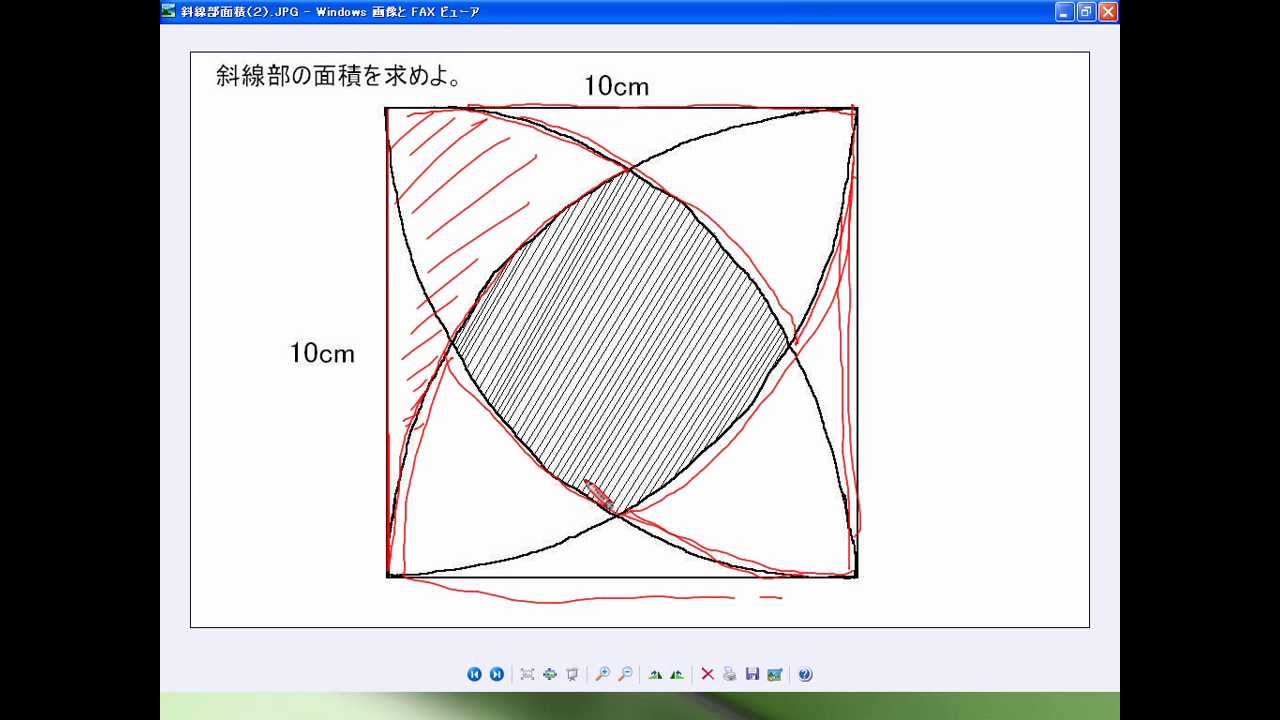
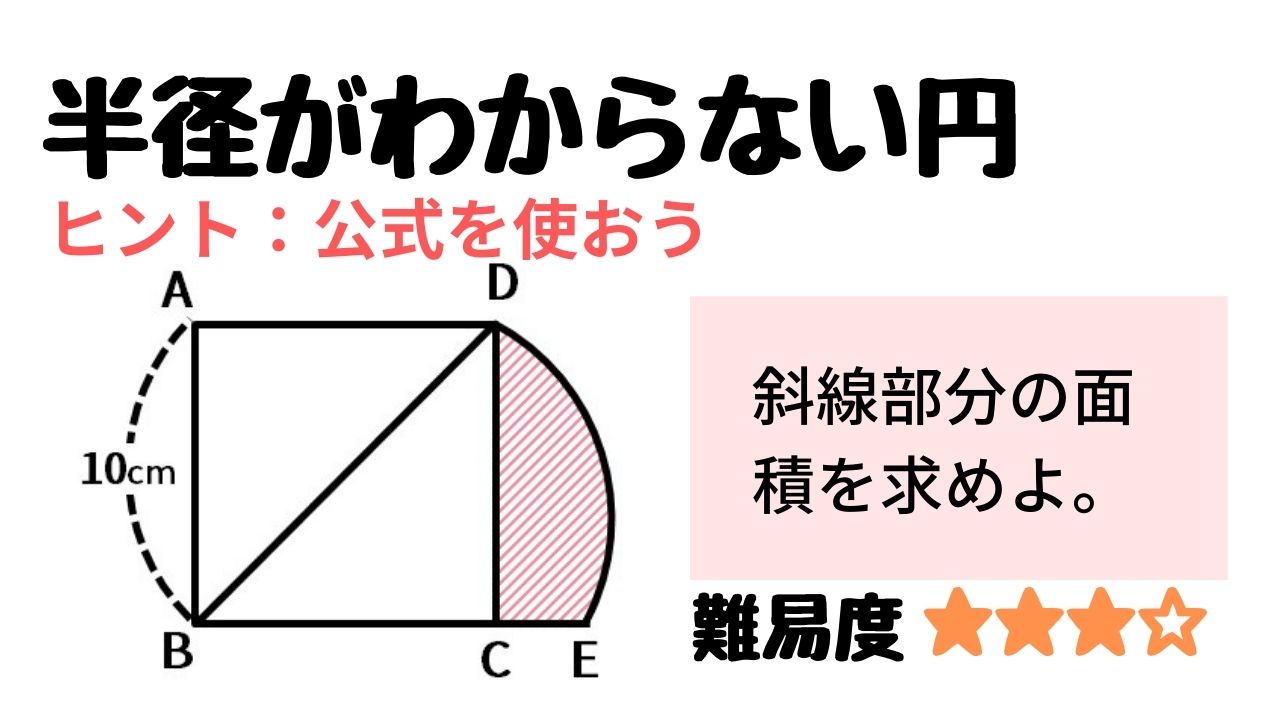
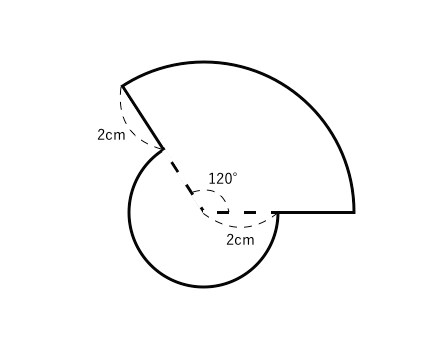
314 = 26 c m 2 と求めることができます。半径×314 円の面積 = 半径 ×例題 半径5cmの半円を、円Aを中心にして、45°回転させました。 黒くぬった部分の面積を求めなさい。おうぎ形の面積 を 求める力 が、理解できていれば、小学生が自分の力で、解答を導けるプリントを作りました♪パパママ向けのヒント解説も行っていますよ♪
円の面積 応用 中学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  | |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
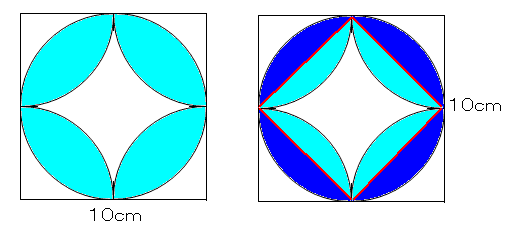 | 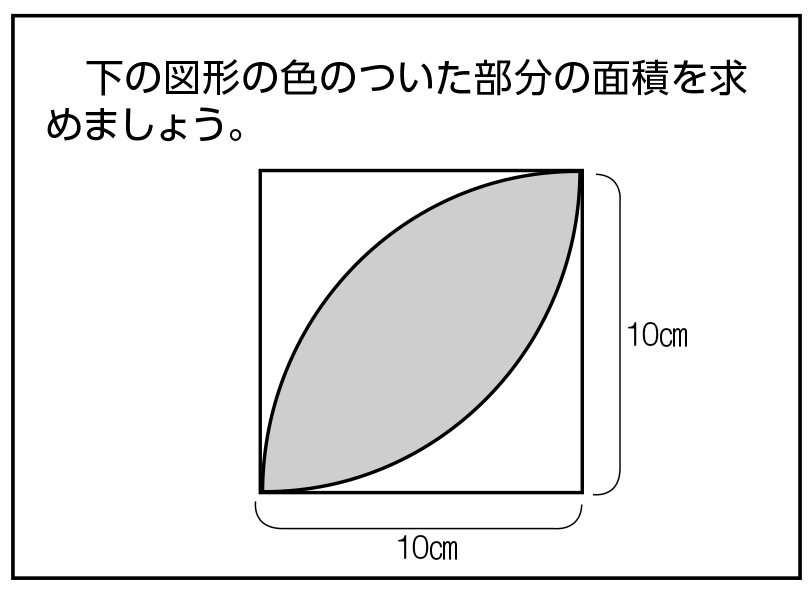 |  |
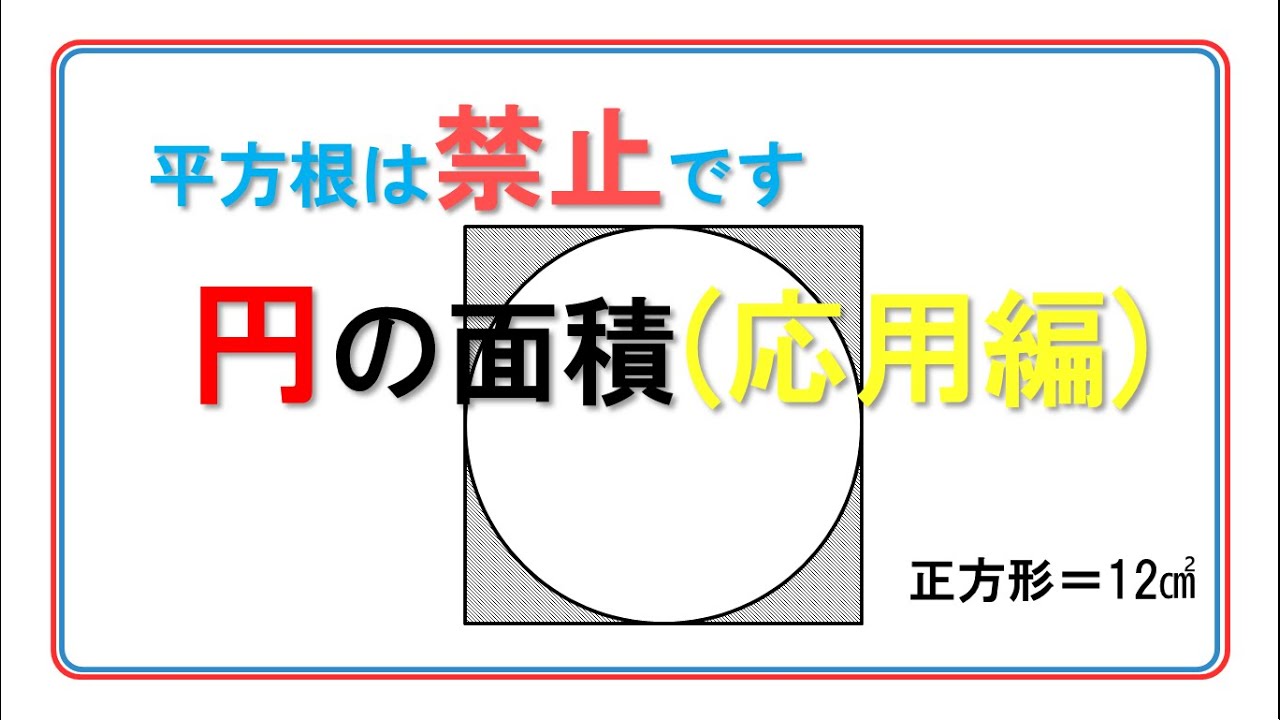 | 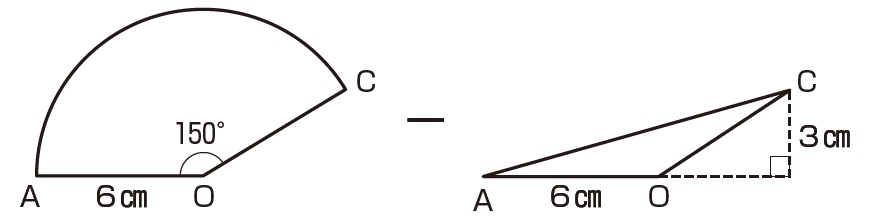 | |
 |  |  |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「円の面積 応用 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
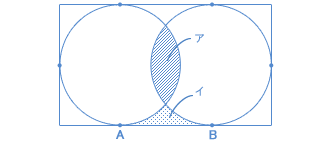 |  |
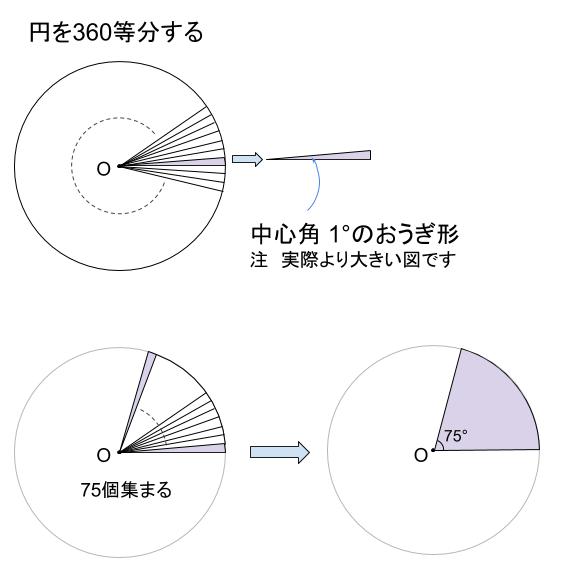
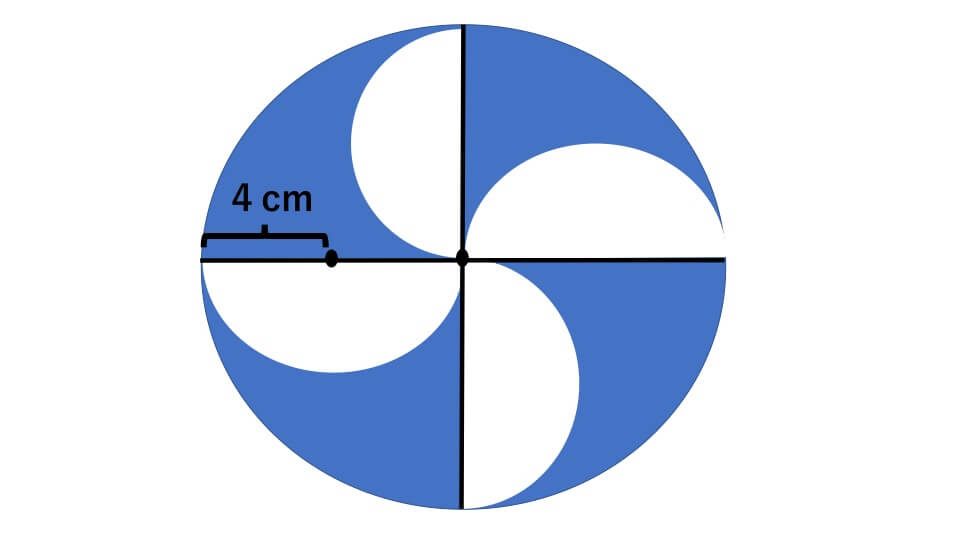
円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr×円の面積の求め方公式 ~円の面積~ (半径)×(半径)×(円周率314) 円の面積公式を理解するためには、図形を見ながら考えていく必要があります。 円を分割して、並びかえると このように平行四辺形に近い形に変形することができるよね。 これ
コメント
コメントを投稿